Das Tor steht fest auf drei Säulen, während der obere Teil von nur zwei Pfeilern getragen wird – eine architektonische Meisterleistung oder nur ein optischer Streich?

Betrachtet man einzelne Bereiche wie z.B. die Sockel der Säulen oder die obere

Querverstrebung für sich alleine, scheinen diese völlig korrekt geformt und angeordnet. Versucht man allerdings, den Sachverhalt „aus drei mach’ zwei“ zu begreife

n, ergibt sich ein Konflikt aus Wahrnehmung und Verstand: das Objekt wird eindeutig wie beschrieben wahrgenommen, unser logisches Denken jedoch sagt „unmöglich“!

Bei der genaueren Betrachtung des unmöglichen Tores fällt auf, dass die oberen beiden Pfeiler aus den Begrenzungen der unteren drei Säulen entspringen. Die Konturen der Säulen bzw. Pfeiler haben bei diesem Modell also eine besondere Bedeutung.

Unsere Wahrnehmung ist es gewohnt, dass Konturen die Begrenzung eines Objektes in eine Richtung darstellen: d.h. auf der einen Seite der Kontur liegt das Objekt, auf der anderen Seite etwas anderes.

Beim Modell des unmöglichen Tores sind die Konturen zweideutig: Die Längskanten bilden einerseits die Abgrenzung der Säulen im unteren Bereich und andererseits die Begrenzung der Pfeiler im oberen Bereich. Und um aus „drei“ Säulen „zwei“ eckige Pfeiler zu erstellen, die seitlich betrachtet werden, sind gleich viele Konturen, nämlich 6 Längskanten notwendig.
Wie kann man ein solches Modell verwirklichen?
Um diese Illusion umzusetzen, ist ein zweiteiliges Modell notwendig:

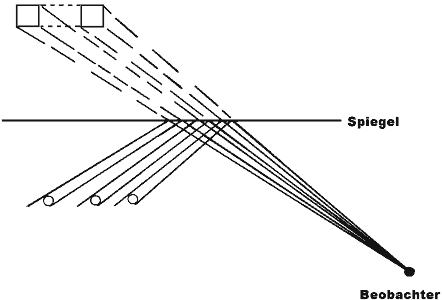
Im vorderen Teil befinden sich die drei Säulen und unsere Bauarbeiter, die mit einer Leuchte im unteren Bereich beleuchtet werden. Dahinter befindet sich ein halbdurchlässiger Spiegel, mit der spiegelnden Seite nach vorne, d.h. der Beobachter sieht nicht, was hinter dem Spiegel vor sich geht, jedoch das Spiegelbild der Säulen.

Dies ändert sich aber, wenn hinter dem Spiegel eine Leuchte eingeschaltet wird: der beleuchtete Bereich ist nun für den Beobachter sichtbar. Und in unserem Modell werden hinter dem Spiegel zwei Pfeiler mit einer Querverstrebung im oberen Bereich beleuchtet.

Dadurch, dass das vordere Modell nur unten und das hintere Modell nur oben beleuchtet wird, sind diese beiden Bereiche sichtbar. Da die Rechnung mit der Anzahl der Konturen nur aufgeht, wenn man Pfeiler von der Seite betrachtet (von vorne würde man zwei Kanten weniger sehen), blickt der Beobachter seitlich auf die Konstruktion.

Damit nun aber beide Modelle fluchtend hintereinander erscheinen, wird das Säulenmodell so angeordnet, dass der Beobachter nur das Spiegelbild sieht. An dem Ort, an dem das Spiegelbild der Säulen erscheint, steht das reale Modell der Pfeiler.

Der Beobachterblickpunkt und die Maße der Modelle wurden dabei so gewählt, dass die einzelnen Seiten und die Zwischenräume der Pfeiler gleich groß erscheinen und dem Durchmesser der Säulen entsprechen.28

Literaturverweise:
28 Monokulare optische Täuschungen – U. Gössel – 1999; auch die Skizze wurde aus dieser Arbeit entnommen

Autor: Prof. Dr. Bernd Lingelbach