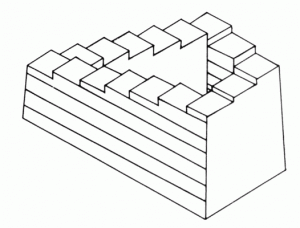
Haben Sie schon einmal versucht, ein Dreieck mit drei rechten Winkeln zu zeichnen?

Die Abbildung trotzt allen geometrischen Prinzipien:

betrachtet man jeweils nur den Bildausschnitt an einer Ecke, erkennt man einen aus zwei Balken gebildeten rechten Winkel; dies ist bei allen drei Ecken der Fall. Nach Adam Riese ergibt das eine Winkelsumme von 270° – das Ergebnis allerdings ist weniger im Sinne der Mathematik, denn ein Dreieck hat stets eine Winkelsumme von 180°.

Die einzelnen Strukturen wie die Ecken vermitteln jeweils einen bestimmten Tiefeneindruck, der durch das räumliche Sehen und andere Tiefenmerkmale wie Schattenverlauf, Perspektive usw. hervorgerufen wird.
Der daraus abgeleitete Verlauf der Balken widerspricht dem Gesamteindruck eines Dreieckes; trotzdem erkennt die Wahrnehmung nicht, dass dieses Objekt unmöglich ist. Erst durch logische Denkvorgänge bemerkt der Beobachter diese Tatsache.

Wie ist das „Dreieck“ konstruiert?

Betrachtet man die Konstruktion des Modells von der Seite, erkennt man den Trick der Täuschung: nur unter einem bestimmten Blickwinkel erscheint der Längsbalken mit den beiden Schenkeln wie ein Dreieck, wird also auf der Netzhaut auch als solches abgebildet.

Und das Wahrnehmungssystem ist gewohnt, dieses Netzhautbild nur auf eine Weise, nämlich als Dreieck zu interpretieren. Auch die wahrgenommenen Tiefeneindrücke der Ecken schaffen es nicht, das Dreieck aufzubrechen, damit wir es als ein anderes Objekt erkennen. Werden die Tiefenwahrnehmung (Stereopsis) und die oben beschriebenen sog. sekundären Tiefenmerkmale ausgeschaltet, verschwindet auch die Unmöglichkeit der Figur: ein gewöhnliches Dreieck bleibt übrig.
Das um 1934 von O. Reutersvärd eher zufällig entdeckte

unmögliche Dreieck ist nur eine von vielen unmöglichen Objekten. Zu den Bekanntesten gehört die Penrose-Treppe (führt denjenigen, der sie hinauf- oder hinabsteigt, wieder zum Ausgangspunkt), der unmögliche Würfel oder Teufelsgabel (drei Zinken sind oben zu sehen, während unten nur zwei aus dem Schaft laufen).

Auswahl einiger unmöglicher Figuren
Natürlich können hier nicht alle bekannten Täuschungen dieser Art und ihre zahlreichen Varianten aufgeführt werden –
ein Besuch der aufgeführten Links im Hauptmenü lohnt sich auf jeden Fall!

Die Penrose-Treppe

Geht man diese Treppe hinauf oder hinab, landet man immer wieder am Ausgangspunkt.
Veröffentlicht wurde diese Figur 1958 mit anderen unmöglichen Objekten von L.S. und R. Penrose.
(Ich sehe was, was du nicht siehst – J.R. Block/H.E. Yuker – 1993)
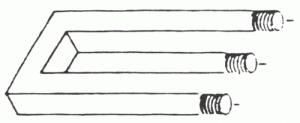Die Teufelsgabel

Diese Version wurde 1964 von D.H. Schuster entwickelt. Obwohl links nur zwei Balken zu sehen sind, endet die Struktur mit drei Zapfen.
(Ich sehe was, was du was du nicht siehst – J.R. Block/H.E. Yuker – 1993)
Treppauf, Treppab

Die klassischen unmöglichen Objekte dienten außerdem vielen Künstlern als Grundlage für ihre Bilder, z. B. M.C. Escher oder Sandro Del-Prete.
Grundelement dieser Lithografie von M.C. Escher ist die Penrose-Treppe.
(www.worldofescher.com – 27.06.00)
Die Quadratur des Kreises

In dieser Bleistiftzeichnung von Sandro Del-Prete sind zwei unmögliche Dreiecke enthalten.

Autor: Prof. Dr. Bernd Lingelbach