Welcher der beiden Querbalken ist länger? Man kann sich dem Eindruck nicht entziehen, dass die obere Querlinie länger ist als die untere – tatsächlich sind aber beide gleich lang!

Die bekannte, klassische Ponzo-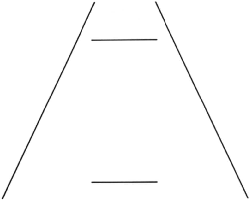Täuschung wurde 1928 von M. Ponzo entdeckt.16 Bei der Originalfigur beträgt die Täuschung etwa 10-15% der Linienlänge.17 Die Illusion selbst wird durch die konvergenten Linien verursacht.

Wie entsteht die Fehleinschätzung der Querbalken?

Eine Theorie, die sog. Kontrasttheorie, geht davon aus, dass sich benachbarte Figurelemente beeinflussen – und zwar dahingehend, dass Unterschiede zwischen den einzelnen Elementen verstärkt werden.17 In der Ponzo-Figur füllt die untere Querlinie nur einen geringen Teil der Fläche zwischen den konvergenten Geraden aus und wird darum verkleinert wahrgenommen.

Analog wird der obere Querbalken durch den geringen Abstand zu den konvergenten Linien vergrößert wahrgenommen.

Die sog. Assimilationstheorie geht ebenfalls von einer gegenseitigen Beeinflussung der Einzelkomponenten aus – allerdings in der Weise, dass sich die Elemente einander angleichen.

In der klassischen Ponzo-Figur wird demnach die obere Querlinie mit den Schrägen in Zusammenhang gebracht und dadurch gestreckt, was einer Angleichung des Querbalkens an den Abstand der konvergenten Linien entspricht.17

Um den Effekt der Assimilation und des Kontrasts 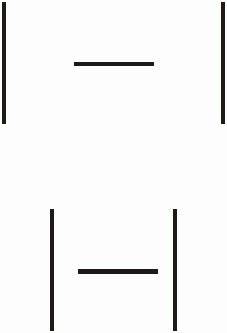bei der Ponzo-Figur zu testen, wurde die nebenstehende Figur entwickelt. Dort kann zwar eine Täuschung ausgelöst werden, sie fällt allerdings weit geringer aus als bei der Ponzoschen Originalfigur. Dies lässt darauf schließen, dass für die Illusion noch ein weiterer Mechanismus verantwortlich ist.

Derzeit sind viele Wissenschaftler der Auffassung, dass die Illusion durch eine räumliche Verarbeitung der Figur zustande kommt. Dies ist naheliegend, da die Linienkonfiguration auch im Alltag im Rahmen der perspektivischen Abbildung (z.B. als Netzhautbild) vorkommt.

Die beiden Schrägen simulieren hierbei parallele Linien, die sich aufgrund der Gesetze der Perspektive im Unendlichen einander annähern, d.h. auf einen Fluchtpunkt zulaufen (ähnlich wie bei der Betrachtung von Eisenbahnschienen, die sich ebenfalls mit zunehmender Entfernung anzunähern scheinen).

Im Alltag sind wir außerdem gewohnt, dass Objekte mit zunehmender Entfernung kleiner werden. Erzeugt ein fernes Objekt ein Netzhautbild gleicher Größe wie ein nahes Objekt, geht unser Wahrnehmungssystem davon aus, dass das weiter entfernte Objekt größer sein muss – die Informationen von Netzhautbildgröße und wahrgenommener Entfernung werden also miteinander verrechnet (Emmertsches Gesetz).17

Bei der Ponzo-Täuschung wird durch die Schrägen ebenfalls eine Tiefenwahrnehmung induziert – die dem Beobachter allerdings nicht bewusst sein muss.

Da die obere Querlinie dadurch weiter entfernt erscheint (bei gleicher Netzhautbildgröße, die bei der unteren Querlinie entsteht), nimmt der Beobachter die obere Linie größer wahr.

Für diese Theorie spricht, dass die Täuschung umso stärker wird, je realistischer die Szene dargestellt ist (d.h. je mehr monokulare Tiefenmerkmale vorhanden sind).17

Außerdem wurde in Untersuchungen festgestellt, dass Menschen, die außerhalb der westlichen Tradition (in der die Linearperspektive selbstverständlich ist) aufgewachsen sind – also z.B. Afrikaner, in deren Umwelt rechte Winkel und exakt gerade Linien weit seltener vorkommen – sich nicht so stark durch die Ponzo-Figur täuschen lassen.14

Allerdings kann die Tiefenwahrnehmung nicht die einzige Ursache für die Illusion sein:
Selbst wenn mit Hilfe einer stereoskopischen Abbildung der obere Querbalken eindeutig weiter vorne liegt als der untere, lässt sich die Täuschung nicht vollständig unterdrücken.17

Literaturverweise:
16 Macht schwarz schlank? – J. Ninio – 1999
17 Wahrnehmung – I. Rock – 1985
14 Unglaubliche optische Illusionen – N. Rodgers – 1998
Die Abbildung mit den Eisenbahnschienen stammt aus dem Buch Illusionen des Sehens – T. Ditzinger – 1997
Autor: Prof. Dr. Bernd Lingelbach